Taken from Krahula's One Zentangle A Day
Dimension
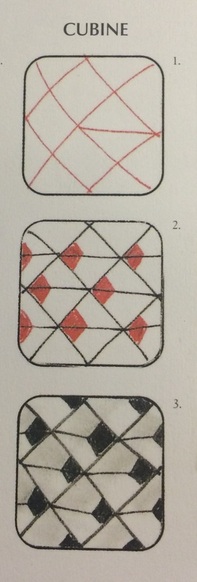
The Cubine pattern takes advantage of angles in order to create a two-dimensional pattern that looks three-dimensional. In order to make the pattern look truly 3-D, you have to use some math! The math in this one is a little simpler, but it's interesting because many simple mathematical principles of geometry are used to create the perception of extra dimension.
Parallel Lines
To start to make the pattern, you must first draw a grid of parallel lines. More parallel lines cut horizontally through the points of intersection of the first sets of parallel lines. So far, we have three sets of parallel lines--each set going a different direction.
Similar Shapes
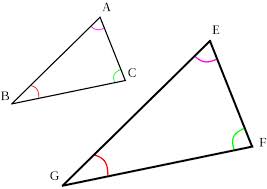
Now look at the photograph of the steps for drawing the pattern. The photo shows diamonds, and if you tilt your head, you can see squares--or maybe cubes! Each smaller shaded rhombus is drawn by creating short lines parallel to the non-horizontal sets of parallel lines. Because the small, shaded rhombuses have the same angles as the larger rhombuses, the small and large rhombuses are called "similar rhombuses." They have the same proportions. Usually, we learn about similar triangles, which is a similar concept. Below is a diagram of similar triangles:
The Cubine pattern takes advantage of angles in order to create a two-dimensional pattern that looks three-dimensional. In order to make the pattern look truly 3-D, you have to use some math! The math in this one is a little simpler, but it's interesting because many simple mathematical principles of geometry are used to create the perception of extra dimension.
Parallel Lines
To start to make the pattern, you must first draw a grid of parallel lines. More parallel lines cut horizontally through the points of intersection of the first sets of parallel lines. So far, we have three sets of parallel lines--each set going a different direction.
Similar Shapes
Now look at the photograph of the steps for drawing the pattern. The photo shows diamonds, and if you tilt your head, you can see squares--or maybe cubes! Each smaller shaded rhombus is drawn by creating short lines parallel to the non-horizontal sets of parallel lines. Because the small, shaded rhombuses have the same angles as the larger rhombuses, the small and large rhombuses are called "similar rhombuses." They have the same proportions. Usually, we learn about similar triangles, which is a similar concept. Below is a diagram of similar triangles:
http://www.maa.org/publications/periodicals/convergence/proportionality-in-similar-triangles-a-cross-cultural-comparison-the-student-module
Lines of Symmetry
Interestingly, the horizontal parallel lines act as lines of symmetry in the pattern. The other parallel lines do not because of where the shaded rhombuses are positioned. The lines of symmetry draw the eye into the shaded rhombuses, and the shaded rhombuses appear to be farther away. The Cubine pattern shows a way that geometry can create illusions--and you use geometry sometimes without thinking when you are doodling!
