 Taken from Krahula's One Zentangle A Day
Taken from Krahula's One Zentangle A Day
Infinite Series
What is an infinite series?
An infinite series is a series of an infinite number of terms that follow a pattern. As more terms are added, the sum of the terms gets closer to a number--this number is the limit.
What does this have to do with Zentangles?
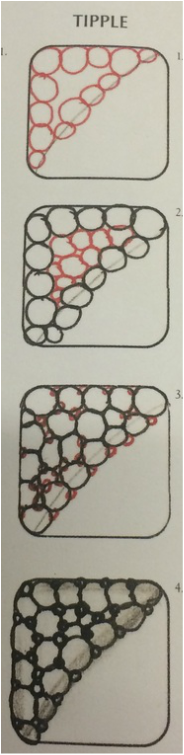
In the Tipple Pattern, different sized circles are drawn. Say you decide to draw the Tipple pattern and you want to leave the least white space in between the circles as possible. You line some larger circles up in a grid, and then draw circles about half of that size in the white space left. Then you draw circles half of that size (1/4 of the original circle) in the leftover white space, and you continue this. Eventually, you will be unable to draw more circles, but if you could draw perfect circles and very, very small circles, then there would always be white space left. The circles would continue to decrease in size by 1/2. Because of this, the Tipple pattern behaves in a very similar when to an infinite series. Now, let's put this in numerical terms. Say the area of your first circles--the big circles--is 1. The area of the next smallest circle is 1/2, next smallest: 1/4, etc. If you only look at one of each size circle, then the total area of these circles would be: 1+1/2+1/4+1/8+1/16...(1/infinity). This total area number would get closer and closer to two, but never hit it. Therefore, the limit is two. This is the same idea as Zeno's Paradox! More examples of infinite series can be found HERE.
In addition, this pattern can be used to make a fractal: a self similar pattern that looks the same geometrically at different scales (American Heritage Dictionary).
What is an infinite series?
An infinite series is a series of an infinite number of terms that follow a pattern. As more terms are added, the sum of the terms gets closer to a number--this number is the limit.
What does this have to do with Zentangles?
In the Tipple Pattern, different sized circles are drawn. Say you decide to draw the Tipple pattern and you want to leave the least white space in between the circles as possible. You line some larger circles up in a grid, and then draw circles about half of that size in the white space left. Then you draw circles half of that size (1/4 of the original circle) in the leftover white space, and you continue this. Eventually, you will be unable to draw more circles, but if you could draw perfect circles and very, very small circles, then there would always be white space left. The circles would continue to decrease in size by 1/2. Because of this, the Tipple pattern behaves in a very similar when to an infinite series. Now, let's put this in numerical terms. Say the area of your first circles--the big circles--is 1. The area of the next smallest circle is 1/2, next smallest: 1/4, etc. If you only look at one of each size circle, then the total area of these circles would be: 1+1/2+1/4+1/8+1/16...(1/infinity). This total area number would get closer and closer to two, but never hit it. Therefore, the limit is two. This is the same idea as Zeno's Paradox! More examples of infinite series can be found HERE.
In addition, this pattern can be used to make a fractal: a self similar pattern that looks the same geometrically at different scales (American Heritage Dictionary).
